如何理解quickSort?

最近在复习快排，便重新整理了一下，除了classic quickSort 还有变种quickSelectionSort(随机快排)，如215、1738，还有Dual-Pivot Partition、Three-Way Partition。不同的partition复用，使其在面对不同情况下有不同的效果

最常见的快排，最坏的情况是

1.已经/几乎有序 → 退化成冒泡排序

2.pivot刚好是最大值/最小值

Hoare quickSort,

这个版本的算法在含有许多重复元素的情况下，可以避免其出现最坏情况的划分

public int partition(int[] a , int lo , int hi){
    int p = a[lo];
    int i = lo - 1 , j = hi + 1;
    
   while(true){
       while(a[--j] > p);
       while(a[++i] < p);
       
       if(i < j)
           swap(a , i , j);
       else
           return j ;
   }
}

这是改进后的，也是我们现在最常用的版本

    public void quickSort(int[] arr){
        quickSort(arr , 0 , arr.length - 1);
    }
    
    public void quickSort(int[]arr , int first , int last){
        if (last > first){
            int pivotIndex = partition(arr , first , last);
            quickSort(arr , first , pivotIndex - 1);
            quickSort(arr , pivotIndex + 1, last);
        }
    }

    public int partition(int[]arr , int first , int last){
        int pivot = arr[first];
        int low = first + 1;
        int high = last;

        while (high > low){
            //Search left to right
            while (high >= low && arr[low] <= pivot){
                low++;
            }

            //Search right to left
            while (high >= low && arr[high] > pivot){
                high--;
            }

            if (high > low){  //swap the element in the array
                swap(arr , low , high);
            }
        }

        while (high > first && arr[high] >= pivot){
            high--;
        }

        //swap the pivot
        if (pivot > arr[high]){
            swap(arr , first , high)
            return high;
        }
        else {
            return first;
        }
    }
	
	private void swap(int[] arr , int i , int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

随机化

先洗牌后partition , 随机生成pivot , 然而并没有改变最坏情况下的运行时间，只是减少了出现最坏情况的可能，即无法保证每次pivot都是正中间的索引的。

且quickSelectionSort不关心a[ lo…p - 1] 和 a[p + 1 … hi] 是否有序，此方法一般应用于找Kth Element

private int partition(int[] nums, int lo, int hi) {
        if (lo == hi) {
            return lo;
        }
        int pivot = nums[lo];
        // j = hi + 1 因为 while 中会先执行--
        int i = lo, j = hi + 1;

        while (true) {
            // 保证 nums[lo..i] 都小于 pivot
            while (nums[++i] < pivot) {
                if (i == hi) {
                    break;
                }
            }
            // 保证 nums[j..hi] 都大于 pivot
            while (nums[--j] > pivot) {
                if (j == lo) {
                    break;
                }
            }
            if (i >= j) {
                break;
            }

            swap(nums, i, j);
        }

       //交换pivot
        swap(nums, j, lo);
       // 如果走到这里，一定有：
       // nums[i] > pivot && nums[j] < pivot
       // 所以需要交换 nums[i] 和 nums[j]，
       // 保证 nums[low..i] < pivot < nums[j..high]
    
        return j;
}

private void shuffle(int[] nums) {//打乱数组
        int n = nums.length;
        Random ran = new Random();
        for (int i = 0; i < n; i++) {
            int r = i + ran.nextInt(n - i);
            swap(nums, i, r);
        }
}

//another ver.
public int randomPartition(int[] a, int l, int r) {
        int i = random.nextInt(r - l + 1) + l;
        swap(a, i, r);
        return partition(a, l, r);
}

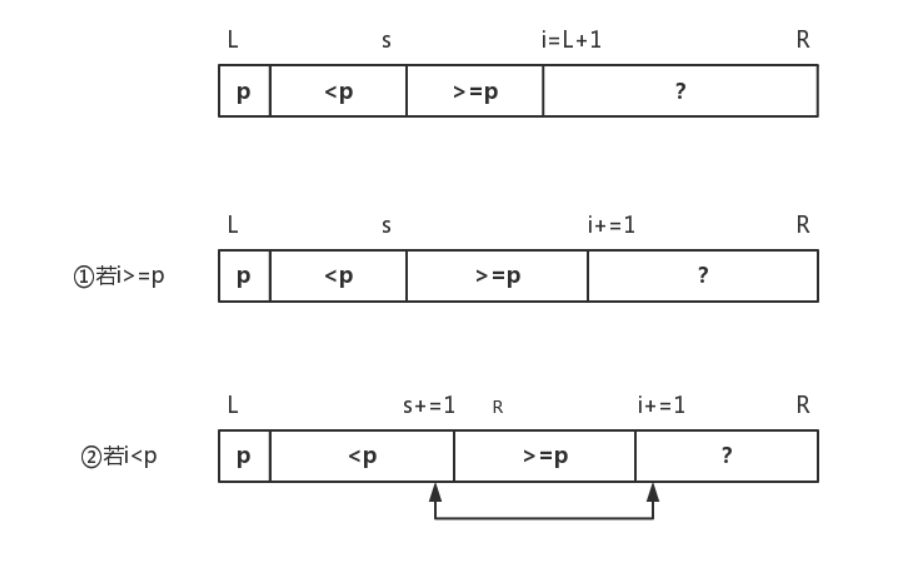
Lomuto划分

一个数组被分成三段，设最左为pivot , 一段是<a[pivot] , 一段>a[pivot] , 还有一段未处理的数据

从左往右扫描数组，将第三段未处理的数据和p比较 , 其中 s 指向 第一段末尾 ， i 指向 第二段末尾

若val >= a[p] 则 i++ / 若val <= a[p] , 则需要s++ ，并和a[i]互换 ,然后 i++ ，继续指向尾端

直到第三段为空，a[s] 与 a[pivot] 交换

public void quickSort(int[] a , int l , int r){
    if(l < r){
        int p = partition(a , l , r);
        quickSort(a , l , p - 1);
        quickSort(a , p + 1 , r);
    }
}

private int partition(int[] a ,int l, int r) {
        int p = a[l];
        int s = l;
        for (int i = l + 1; i <= r; i++) {
            if (a[i] < p) {
                s = s + 1;
                int temp = a[s];
                a[s] = a[i];
                a[i] = temp;
            }
        }
        int temp = a[l];
        a[l] = a[s];
        a[s] = temp;
        return s;
}

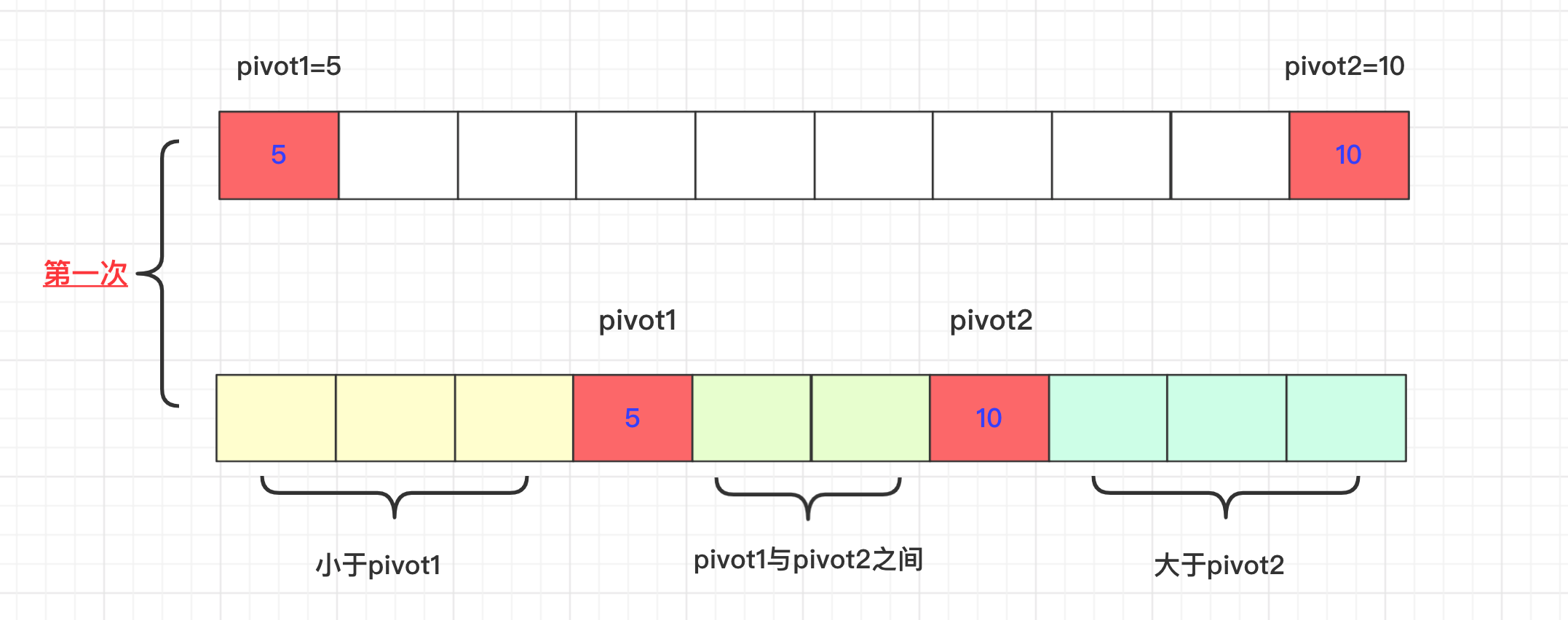
Dual-Pivot Partition

Arrays.sort()就是用该方法实现的

对于长度小于17的数组使用插入排序(常见优化步骤，传统快排也有应用)。
选择两个枢纽元p1,p2，一般选择起始元素a[left]和末尾元素a[right]（有其他选取方式）。
假设p1<p2，如果不是就交换。
将整个数组分成三部分，分别为 <p1的 , p1<X<p2 , >p2 的。
递归排序这三个部分。

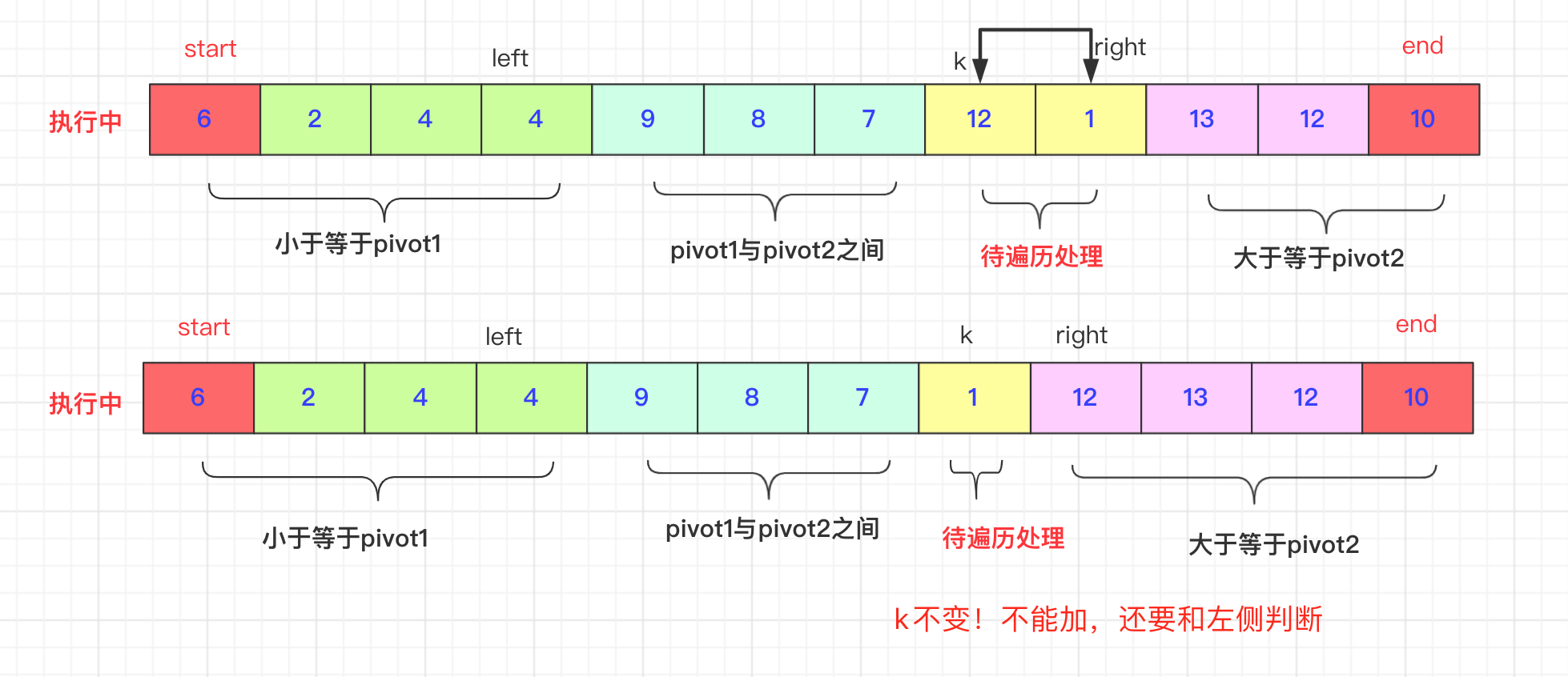
这样进行一次后递归的进行下一次双轴快排，一直到结束，但是在这个执行过程应该去如何处理分析呢？需要几个参数呢？

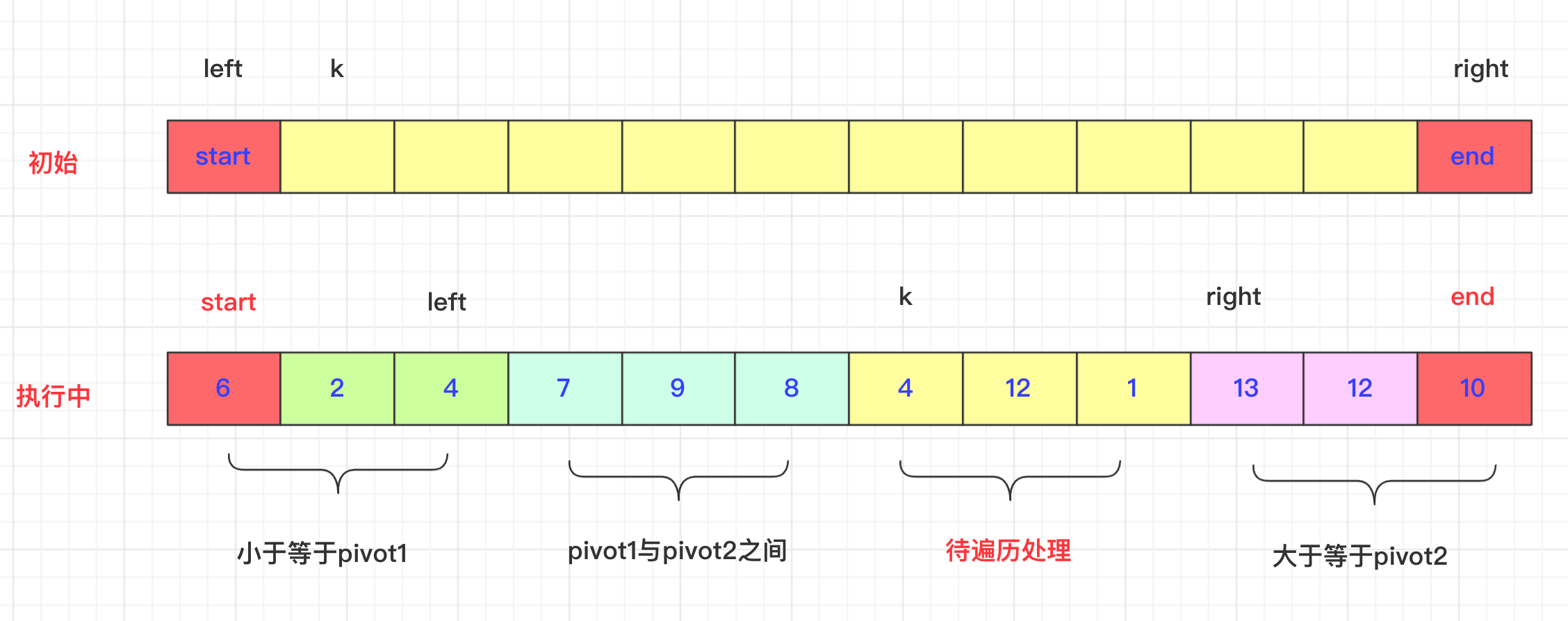
假设知道排序区间[start，end]。数组为arr， pivot1=arr[start],pivot2=arr[end]
还需要三个参数left，right和k。 l
left初始为start，[start,left]区域即为小于等于pivot1小的区域(第一个等于)。
right与left对应，初始为end，[right,end]为大于等于pivot2的区域(最后一个等于)。
k初始为start+1，是一个从左往右遍历的指针，遍历的数值与pivot1，pivot2比较进行适当交换，当k>=right即可停止。

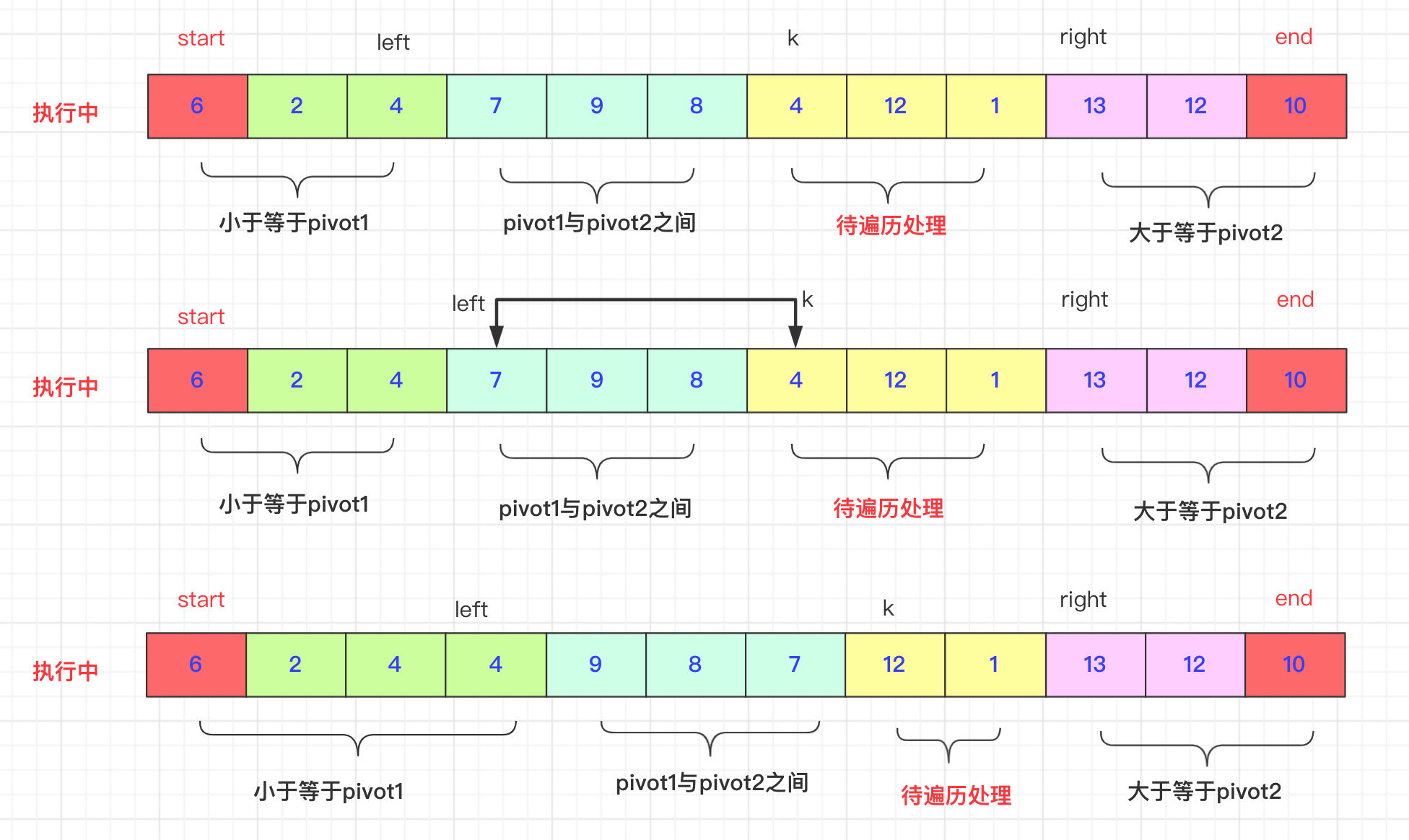
k交换过程然后你可能会问k遍历时候究竟怎么去交换？left和right该如何处理呢？不急我带你慢慢分析，首先K是在left和right中间的，遍历k的位置和pivot1，pivot2进行比较：如果arr[k]<pivot1,那么先++left，然后swap(arr,k,left),**因为初始在start在这个过程不结束start先不动。**然后k++；继续进行

而如果arr[k]>pivot2.(区间自行安排即可) 有点区别的就是right可能连续的大于arr[k],比如9 3 3 9 7如果我们需要跳过7前面9到3才能正常交换，这和快排的交换思想一致，当然再具体的实现上就是right–到一个合适比arr[k]小的位置。然后swap(arr,k,right)**切记此时k不能自加。**因为带交换的那个有可能比pivot1还小要和left交换。如果是介于两者之间，k++即可

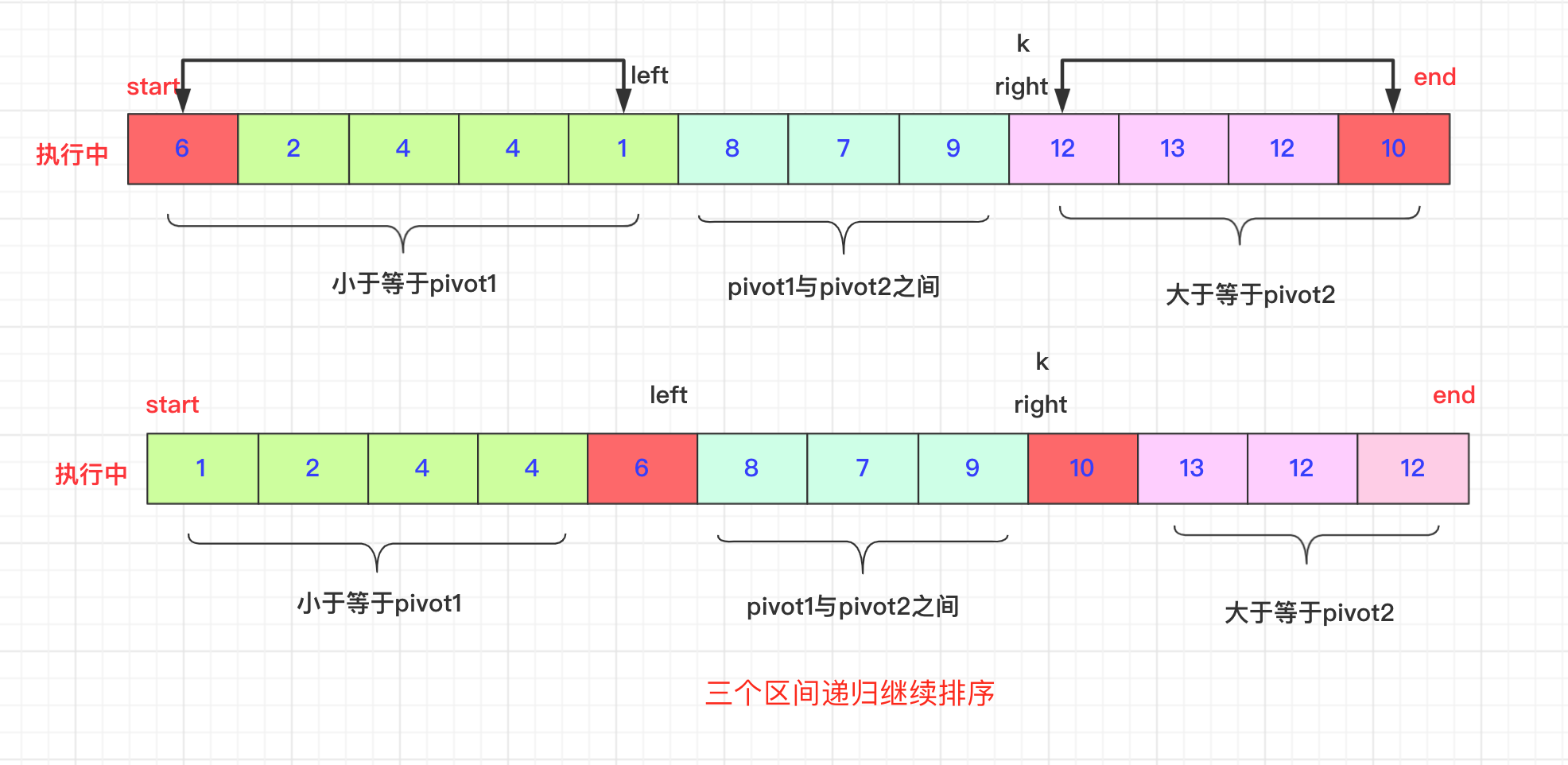
最后则是在执行完这一趟即k=right之后，即开始需要将pivot1和pivot2的数值进行交换

swap(arr, start, left);
swap(arr, end, right);

然后三个区间根据编号递归执行排序函数即可。

public void dualPivotQuickSort(int[] arr, int start, int end) {
        if(start > end){
            return;
        }
        if(arr[start] > arr[end])
            swap(arr, start, end);
        int pivot1 = arr[start] , pivot2 =a rr[end];
    	//取最左侧和最右侧作为pivot
        //(start，left]:左侧小于等于pivot1 [right,end)大于pivot2
        int left = start , right = end, k = left + 1;
        while (k < right) {
            //和左侧交换
            if(arr[k] <= pivot1)
            {
                //需要交换
                swap(arr, ++left, k++);
            }
            else if (arr[k]<=pivot2) {//在中间的情况
                k++;
            }
            else {
                while (arr[right]>=pivot2) {//如果全部小于直接跳出外层循环
                    if(right--==k)
                        break ;
                }
                if(k>=right)break ;
                swap(arr, k, right);
            }
        }
        swap(arr, start, left);
        swap(arr, end, right);
    	//分段递归，继续排序
        dualPivotQuickSort(arr, start, left-1);
        dualPivotQuickSort(arr, left+1, right-1);
        dualPivotQuickSort(arr, right+1, end);
    }

private void swap(int arr[],int i,int j){
        int team=arr[i];
        arr[i]=arr[j];
        arr[j]=team;
}

Three-Way Partition ，三路快排 , Dijkstra / Bentley-McIlroy

以最左元素、最右元素、最中间元素为pivot ，在双轴快排的基础上，在分一个等于p的区段

private void sort(Comparable[] arr, int l, int r){
        // 对于小规模数组, 使用插入排序
        if(r - l <= 15){
            InsertionSort.sort(arr, l, r);
            return;
        }
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap(arr, l, (int)(Math.random()*(r-l+1)) + l );
 
        Comparable v = arr[l];
 
        int lt = l;     // arr[l+1...lt] < v
        int gt = r + 1; // arr[gt...r] > v
        int i = l + 1;    // arr[lt+1...i) == v
        while(i < gt){
            if(arr[i].compareTo(v) < 0){
                swap( arr, i, lt + 1);
                i++;
                lt++;
            } else if(arr[i].compareTo(v) > 0){
                swap(arr, i, gt - 1);
                gt--;
            } else{ // arr[i] == v
                i++;
            }
        }
 
        swap(arr, l, lt);
        sort(arr, l, lt-1);
        sort(arr, gt, r);
}
 
private void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
}

Dijkstra / Bentley-McIlroy的源码 , 在无重复值的情况下，Bentley-McIlroy方法相较于双轴快排，由于头尾只有少量的等值元素需要交换，所以额外的开销很小。

// Dijkstra 3-way partitioning
private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return;
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo+1;
    while (i <= gt)
    {
        int cmp = a[i].compareTo(v);
        if      (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else              i++;
    }
    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

// Bentley-McIlroy 3-way partitioning
private static void sort(Comparable[] a, int lo, int hi) { 
    int i = lo, j = hi+1;
    int p = lo, q = hi+1;
    Comparable v = a[lo];
    while (true) {
        while (less(a[++i], v))
            if (i == hi) break;
        while (less(v, a[--j]))
            if (j == lo) break;

        // pointers cross
        if (i == j && eq(a[i], v))
            exch(a, ++p, i);
        if (i >= j) break;

        exch(a, i, j);
        if (eq(a[i], v)) exch(a, ++p, i);
        if (eq(a[j], v)) exch(a, --q, j);
    }

    i = j + 1;
    //多了交换的步骤
    for (int k = lo; k <= p; k++)
        exch(a, k, j--);
    for (int k = hi; k >= q; k--)
        exch(a, k, i++);
}